Memahami relativiti. (3)

Relativiti Galilei dan Relativiti Einstein.

Postulat kedua dalam teori relativiti khas;
“Halaju cahaya dalam ruang kosong (hampagas) adalah pemalar mutlak dalam alam dan bebas daripada gerakan jasad yang memancarkannya.”
- Albert Einstein (1879-1955)

Perhatikan rajah di bawah.



Rajah di atas menunjukkan sebuah bola di atas sebuah landasan TANPA GESERAN atau landasan licin mutlak. Pemerhati berada di hujung landasan bertanda B sementara hujung landasan satu lagi bertanda A. Bola bergerak dari A ke B dengan halaju V. Katakan landasan tersebut pegun. Maka halaju bola dari A menuju ke pemerhati (iaitu B) ialah V.

Bagaimana jika landasan turut sama bergerak dengan halaju seragam? (lihat rajah di bawah)


Kes 1: Landasan menjauhi pemerhati


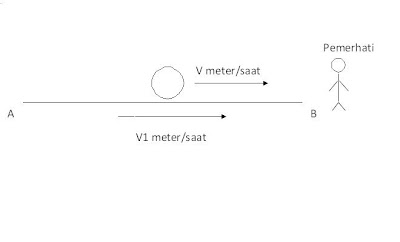
Kes 2: Landasan mendekati pemerhati

Katakan halaju landasan ialah V1 dan bola masih bergerak di atasnya dengan halaju V, maka

Jika landasan bergerak menjauhi pemerhati;
Halaju bola yang baru, V2 = V-V1, untuk V>V1

Jika landasan bergerak mendekati pemerhati;
Halaju bola yang baru, V2 = V+V1

(rumus-rumus di atas mengikut kebiasaan (English-common sense) yang mana bola atas landasan yang mendekati pemerhati sampai lebih cepat berbanding jika ia di atas landasan yang sedang menjauhi pemerhati)

Pengiraan halaju relatif suatu jasad dengan teknik penambahan dan penolakan dari halaju bingkai rujukan seperti di atas ialah teknik yang diperkenalkan dalam teori relativiti oleh Galileo Galilei, seorang ahli astronomi Itali pada era Renaissance. Semenjak penemuan relativiti khas oleh Einstein pada 1905 maka teori Galilei tidak lagi digunapakai terutama dalam penyelidikan nuklear. Ini kerana dalam dunia atom, zarah-zarah bergerak pada laju yang hampir dengan laju cahaya, di mana pada laju ini relativiti khas menjadi ketara. (English-significant)

Jika bola tersebut digantikan dengan alur cahaya yang bergerak dengan halaju c, adakah apabila landasan bergerak dengan halaju V1, maka halaju cahaya sama dengan c+V1 atau c-V1 sebagaimana contoh di atas? Menurut Einstein menerusi postulat keduanya, IA TIDAK BERLAKU.

Oleh itu, tidak kira sama ada landasan bergerak menjauhi atau mendekati pemerhati, ia tetap sampai kepada pemerhati pada satu tempoh masa YANG SAMA. Cahaya akan tetap bergerak dengan halaju c. Halaju landasan tidak akan memberikan apa-apa kesan terhadap halaju cahaya.

Kesan postulat kedua relativiti khas terhadap keserentakan dua peristiwa.

**Eksperimen di bawah tidak pernah dijalankan. Ini kerana ia tidak praktikal dalam dunia realiti dan direka khas untuk tujuan pemahaman sahaja. (lihat bahagian Praktikaliti Eksperimen di bawah)

Rajah di bawah menunjukkan sebuah tren sedang bergerak dengan halaju V meter/saat. Pada masa yang sama dua alur cahaya dipancarkan dari pusat tren, O menuju ke A dan B, ketika pemerhati di luar tren bersetentang dengan O. Jarak OB dan OA ialah c meter. Pemerhati dalam tren mendapati cahaya bergerak dengan halaju c meter/saat. Maka dia menyimpulkan bahawa kedua-dua cahaya sampai ke A dan B serentak.

Klik untuk imej lebih besar

Menurut teori Galilei, halaju cahaya ke B ialah (c-V)meter/saat dan ke A ialah (c+V)meter/saat, jika diukur oleh pemerhati di luar tren. Selepas satu saat, jarak B dari pemerhati ialah (c-V)meter manakala jarak A dari pemerhati ialah (c+V)meter. Oleh itu, selepas satu saat, kedua-dua cahaya sampai ke A dan B serentak menurut pemerhati di luar tren.

Namun menurut teori Einstein, halaju cahaya ke B dan ke A masing-masing ialah c meter/saat jika diukur oleh pemerhati di luar tren. Ini kerana halaju cahaya mesti sama dalam semua bingkai rujukan. Oleh itu selepas satu saat, situasi berlainan berlaku. (lihat rajah kedua di bawah)

klik untuk imej lebih besar

Jika cahaya bergerak dengan halaju c meter/saat menurut pemerhati luar tren, maka selepas satu saat, cahaya akan menembusi B dan keluar dari tren, sementara satu lagi alur cahaya tidak sampai ke A. Tetapi apa yang dilihat oleh pemerhati di luar tren ialah, cahaya sampai ke B dan A sepertimana situasi pertama tanpa sebarang penembusan atau penamatan di tengah-tengah perjalanannya. Dengan kata lain,

Cahaya dari O ke B melalui jarak (c-V)meter pada masa kurang dari sesaat agar halaju cahaya dikekalkan sebagai c meter/saat pada pemerhati di luar tren.

Cahaya dari O ke A melalui jarak (c+V)meter pada masa lebih dari sesaat agar halaju cahaya dikekalkan sebagai c meter/saat pada pemerhati di luar tren.

Penjelasan secara matematik

Pertimbangkan hukum matematik di bawah:
A=B/C
Katakan B=24 dan C=2, maka A=12
Bagaimana jika C=3? Maka A=24/3=8.

Di sini jelas menunjukkan apabila A bertambah untuk nilai B yang malar, maka C mesti dikurangkan. Jika A berkurang untuk nilai B yang malar, maka C mesti ditingkatkan.

Hukum matematik di atas boleh digunakan bagi menjelaskan persamaan halaju cahaya dalam tren jika diukur di luar tren.

Cahaya dari O ke B-
Halaju cahaya yang diukur di dalam bingkai rujukan tren:
c meter/saat=c meter/1 saat
Halaju cahaya yang diramalkan akan diperoleh oleh pemerhati di luar tren menurut relativiti Galilei:
(c-V) meter/saat=(c-V)meter/1 saat ,

Untuk nilai (c-V) meter/saat bertambah kepada c meter/saat bagi mematuhi relativiti khas sedang jarak yang dilalui adalah malar iaitu (c-V) meter, maka masa yang diukur oleh pemerhati di luar tren mestilah kurang daripada 1 saat.

Oleh itu, masa yang diukur di luar tren adalah kurang berbanding masa yang diukur di dalam tren untuk cahaya bergerak dari O ke B jika relativiti khas dipatuhi.

Cahaya dari O ke A-
Halaju cahaya yang diukur di dalam bingkai rujukan tren:
c meter/saat=c meter/1 saat
Halaju cahaya yang diramalkan akan diperoleh oleh pemerhati di luar tren menurut relativiti Galilei:
(c+V) meter/saat=(c+V)meter/1 saat ,

Untuk nilai (c+V) meter/saat berkurang kepada c meter/saat bagi mematuhi relativiti khas sedang jarak yang dilalui adalah malar iaitu (c+V) meter, maka masa yang diukur oleh pemerhati di luar tren mestilah lebih daripada 1 saat.

Oleh itu, masa yang diukur di luar tren adalah lebih berbanding masa yang diukur di dalam tren untuk cahaya bergerak dari O ke A jika relativiti khas dipatuhi.

Kesimpulan

Dari analisis di atas terdapat satu kesimpulan penting yang dapat dibuktikan:

Peristiwa yang berlaku serentak menurut pemerhati di dalam tren tidak berlaku secara serentak menurut pemerhati di luar tren.

Fenomena ini hanya KETARA apabila suatu objek bergerak dengan laju yang hampir atau sama dengan laju cahaya. Oleh itu, jika alur cahaya dalam eksperimen di atas digantikan dengan objek seperti bola, peluru dan sebagainya, kedua-dua peristiwa akan nampak berlaku serentak jika dilihat oleh pemerhati di luar tren. Ini kerana objek dalam dunia realiti bergerak dengan kelajuan yang jauh lebih rendah berbanding laju cahaya. Oleh itu, dalam dunia realiti, fenomena tersebut tidak ketara (tetapi tetap berlaku) dan boleh diabaikan.

Praktikaliti eksperimen

Jika menggunakan alur cahaya sepertimana eksperimen di atas, radas yang diperlukan amat sukar untuk dibina dan tidak praktikal, dan persoalan yang sukar sekali untuk diperjelaskan ialah bagaimana mengukur halaju alur cahaya dalam tren dari luar tren? Oleh itu, eksperimen di atas adalah tidak praktikal dan direka sekadar untuk tujuan pemahaman sahaja.

Namun saintis tidak pernah berputus asa dan sentiasa mencari jalan bagi mencari eksperimen-eksperimen yang lebih praktikal bagi membuktikan relativiti khas. Pada awal kurun ke 20-an saintis mula menyedari bahawa fenomena objek yang bergerak dengan kelajuan hampir dengan laju cahaya hanya berlaku pada partikel atau zarah terutama dari bahan radioaktif.

Dengan penemuan tersebut, maka saintis menemui jalan bagi mensimulasi objek dengan pergerakan pada halaju cahaya dalam makmal. Salah satu dari ratusan eksperimen yang dijalankan bagi membenarkan teori relativiti khas adalah Eksperimen Rossi-Hall yang berjaya membuktikan kewujudan dan kebenaran relativiti khas menggunakan sinaran muon dari reputan zarah-zarah dari angkasa lepas yang menembusi ionosfera bumi.


Bersambung pada bahagian seterusnya.